Sometimes I need to study linkages given the DH-parameters. It is difficult to always model different 3D linkages every time I have new set of DH-parameters. For this reason I thought of creating a script that models them for me. I have done this before for creating STL models of arbitrary DH-parameters and to create Amrose-Format workcells (which was also scripted). Though, the python script I used to create these STL models are far from reality (you cannot really 3D-Print these models and expect to have a miniature mechanism) and were only used for visualization. What I have now are scripts that create workable models that can be 3D-printed and connected.
At the moment I only have scripts for linkages with revolute joints. Originally I created a script for FreeCAD because I knew that this parametric software has quite an extensive python API (almost anything you could do model in the CAD system you could write in a script!). You can download the scripts (for both FreeCAD and Rhino) here.
I will only explain how you can do this in Windows. Linux users can do the same in FreeCAD if they know where the user program data is located.
Here is how you can use this script in FreeCAD:
Copy the python file (from Freecad folder) to %APPDATA%\FreeCAD\Macro. An example (pretty much the documentation) how to use it is given by the following sample script
import dh_links
al = [50,145,60,30,80,140]
a = [1,0.7488,0.1166,0.4,0.7878,0.3926]
a = [i*100 for i in a]
d = [0,0.3,0.7348,0,1.1705,1.3127]
d = [i*100 for i in d]
for i in xrange(len(a)):
App.newDocument("link")
App.setActiveDocument("link")
dh_links.ADoc = App.ActiveDocument
dh_links.aDoc = App.activeDocument()
print(i)
dh_links.make_link(al[i],a[i],d[i])
dh_links.ADoc.saveAs("C:/temp/link"+str(i+1)+".FCStd")
App.closeDocument("link")
FreeCAD is based on Open Cascade which is known to have weaknesses when it comes to fillets such as chamfer and rounding. It is far from a complete parametric software, but it is at least free and has a very good scripting API (better than some commercial ones). But because of these weaknesses I decided to create a similar script for a commercial CAD software. I thought of Creo or Inventor, however I really wanted to opt for a CAD software that has a good python API. Since I am not really taking advantage of the parametric capabilities I opted for a non-parametric CAD software with a good python API (the only commercial one that I know). I therefore created a similar script for Rhino. Here is how you can use the script in Rhino:
Copy the python file (from Rhino folder) to anywhere where you want to use the script. In the same location where you have this python file, create another python file to use the script. A sample script (equivalent to the example using FreeCAD) is
from dh_links import *
al = [50,145,60,30,80,140]
a = [1,0.7488,0.1166,0.4,0.7878,0.3926]
a = [i*100 for i in a]
d = [0,0.3,0.7348,0,1.1705,1.3127]
d = [i*100 for i in d]
rs.EnableRedraw(False)
for i in xrange(len(a)):
print(i)
make_link(al[i],a[i],d[i])
rs.Command('-_SaveAs "c:\\temp\\link'+str(i+1)+'.stp" _Enter _Enter')
ids = rs.AllObjects()
rs.DeleteObjects(ids)
rs.EnableRedraw(True)
I realize some shortcomings though (besides the fact that Rhino is not parametric). I wasn’t really able to really justify this as much as I wanted. Chamfer and Rounding will require good access to edge IDs of the object and the python API is not as complete as I wanted it to be.
Finally, here are some screenshots of some of the links created
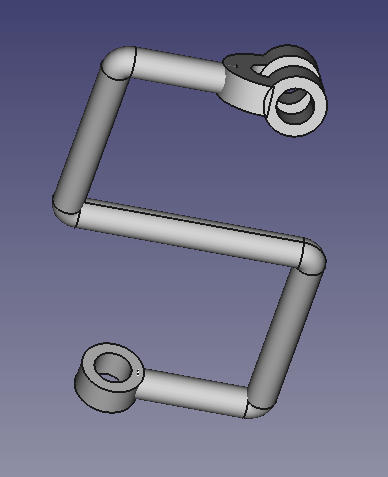
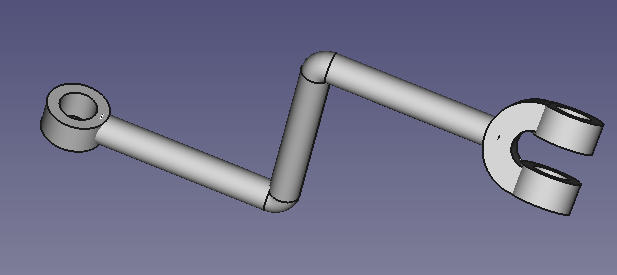
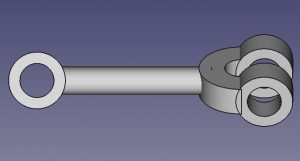
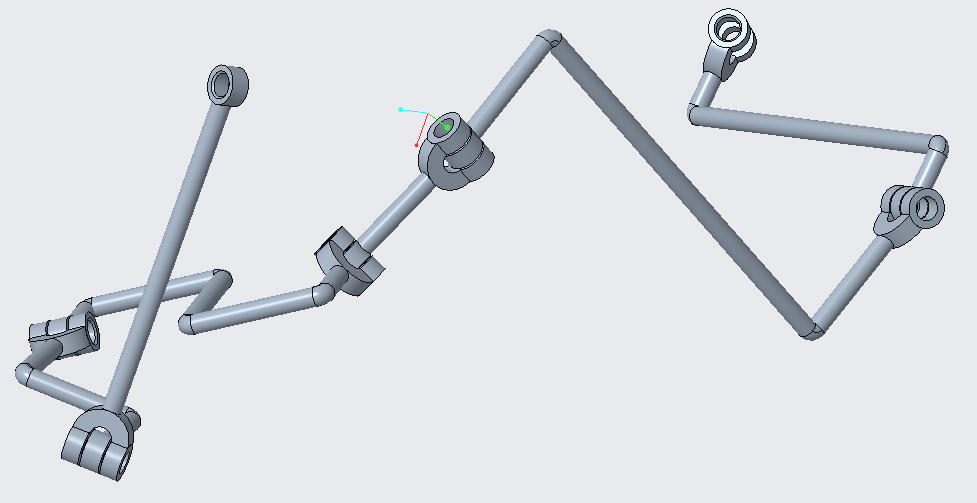
You can then create your own pin to connect links as revolutionary joints (by the design I made, one pin design is sufficient). You can also then combine these links in any CAD software and play around with the linkage there. It is also perfectly all right to just 3D print them and play with them. I’m sure there are bugs and maybe the design may not be robust so feel free to improve on it. Here is a screenshot when I assembled everything (without any screws or pins but with virtual constraints) and played with the linkage in Creo.